lw2333

lw2333

Keep calm and study.
ホームアーカイブ

第四章-多層パーセプトロンMLP

#动手学深度学习101
AI 翻訳
この記事はAIを通じて中国語から日本語に翻訳されました。原文を表示

カバーページ#

非常に印象的なシーンです〜〜

002frieren

MLP の概要#

線形モデルには多くの制約があります～～（明らかなので、ここでは話しません）~~
線形モデルの制約を克服するために、ネットワークに隠れ層を追加することができます。これにより、より一般的な関数の関係を処理できるようになります。最も簡単な方法は、多くの全結合層を積み重ねて、各層を上の層に出力し、最終的な出力を生成することです。最初の L−1L-1 層を表現とし、最後の層を線形予測器と見なすことができます。
このようなアーキテクチャは通常、多層パーセプトロン（multilayer perceptron）またはMLPと呼ばれます。

アフィン関数の合成はアフィン関数であるため（明らかなので）、他の変換を行わずにより多くの線形層を積み重ねることは、非線形学習に対して意味がないです （完全に無意味ではありませんが hh）。

MLP の利点は、アフィン変換の後に各隠れユニットに非線形の活性化関数 activation function σ\sigmaを適用することです。活性化関数の出力は活性値 _activations_と呼ばれます。活性化関数があるため、通常、私たちの多層パーセプトロンを線形モデルに変換することは不可能です。

MLP の構造#

言うまでもありません！

H=σ(XW(1)+b(1)),O=HW(2)+b(2).\begin{aligned} \mathbf{H} & = \sigma(\mathbf{X} \mathbf{W}^{(1)} + \mathbf{b}^{(1)}), \\ \mathbf{O} & = \mathbf{H}\mathbf{W}^{(2)} + \mathbf{b}^{(2)}.\\ \end{aligned}

各隠れ層に非線形の活性化関数を適用した後、隠れ層を積み重ねることは意味があります（より複雑な非線形関係を学習し、より強力な表現能力を持つため）。

H(1)=σ1(XW(1)+b(1))H(2)=σ2(H(1)W(2)+b(2))⋯\begin{aligned} \mathbf{H}^{(1)} &= \sigma_1(\mathbf{X} \mathbf{W}^{(1)} + \mathbf{b}^{(1)})\\ \mathbf{H}^{(2)} &= \sigma_2(\mathbf{H}^{(1)} \mathbf{W}^{(2)} + \mathbf{b}^{(2)})\\ &\cdots \end{aligned}

隠れ層は広げることも深くすることもできますが、選択をしなければなりません （省略）

活性化関数たち#

最初に登場するのは有名な ReLU⁡\operatorname{ReLU} 関数です。非常にシンプルですが、最も広く使用されている活性化関数の一つです。
非常にシンプルで力強いですね。負の値に遭遇すると直接 0 になり、正の値に遭遇するとそのままです。

ReLU⁡(x)=max⁡(x,0).\operatorname{ReLU}(x) = \max(x, 0).

関数のグラフは省略します

しかし、問題があります。 x=0x=0 のときの導関数の値が突然変化します（これは非常に面倒ですが、実際にはすべての境界条件が面倒です）。そのため、私たちは 0 での導関数の値を 0 とデフォルトにします hh、無関心な態度を取ります。

整流ダイオード（信号が通過するか、遮断されるか）に似ています。さらに重要なのは、それがニューラルネットワークの勾配消失問題を解決していることです（）。

「では、一部の信号を通過させるために一部を保持できますか？」
それで、改良版の pReLU⁡\operatorname{pReLU} があります：
pReLU⁡(x)=max⁡(0,x)+αmin⁡(0,x).\operatorname{pReLU}(x) = \max(0, x) + \alpha \min(0, x).

次に登場するのは sigmoid⁡\operatorname{sigmoid} 関数です。sigmoid⁡:R→(0,1)\operatorname{sigmoid}:\mathbb{R}\to(0,1)

sigmoid⁡(x)=11+exp⁡(−x).\operatorname{sigmoid}(x) = \frac{1}{1 + \exp(-x)}.

image

しかし、sigmoid は隠れ層ではあまり使用されておらず、よりシンプルでトレーニングしやすい ReLU に置き換えられています。リカレントニューラルネットワークでは、sigmoid ユニットを使用して時系列情報のフローを制御します。入力が 0 に近づくと、sigmoid 関数は線形変換に近づきます。

ddxsigmoid⁡(x)=exp⁡(−x)(1+exp⁡(−x))2=sigmoid⁡(x)(1−sigmoid⁡(x)).\frac{d}{dx} \operatorname{sigmoid}(x) = \frac{\exp(-x)}{(1 + \exp(-x))^2} = \operatorname{sigmoid}(x)\left(1-\operatorname{sigmoid}(x)\right).

（これは素晴らしい特性です）

最後に紹介するのは tanh⁡\operatorname{tanh} 関数です

tanh⁡(x)=1−exp⁡(−2x)1+exp⁡(−2x).\operatorname{tanh}(x) = \frac{1 - \exp(-2x)}{1 + \exp(-2x)}.

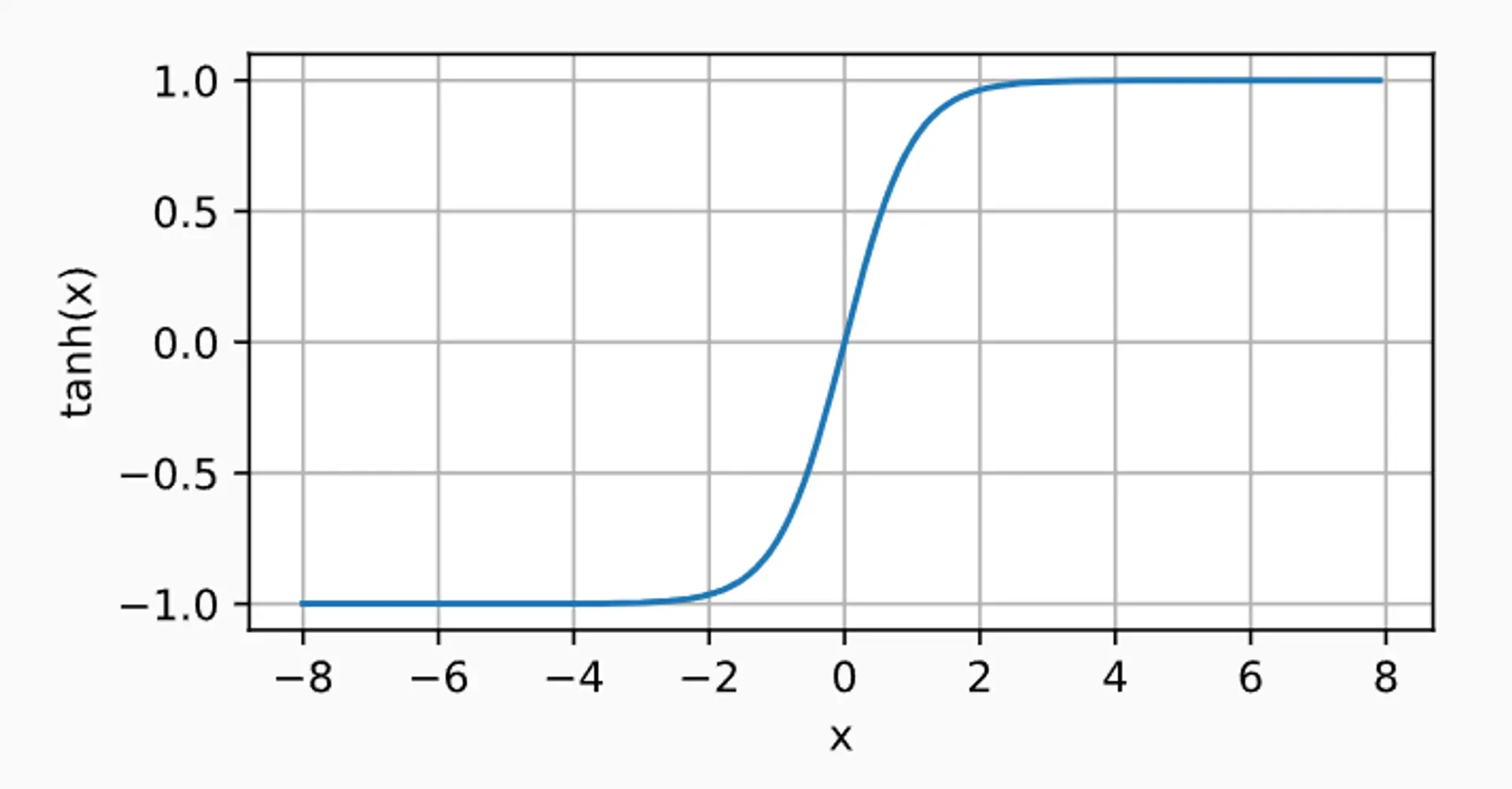
image

ddxtanh⁡(x)=1−tanh⁡2(x).\frac{d}{dx} \operatorname{tanh}(x) = 1 - \operatorname{tanh}^2(x).

（これも素晴らしい特性です）

（偽の）結論#

もちろん、後で補足しますが、とりあえずここまでにしておきます。コードの部分は別のセクションで書くつもりです））
さようならさようなら~

読み込み中...
文章は、創作者によって署名され、ブロックチェーンに安全に保存されています。