一個令人深思的場景~~

MLP 簡介#
線性模型有許多限制 (很明顯,這裡就不講了)
可以在網路中加入隱藏層來克服線性模型的限制,使其能處理更普遍的函數關係。最簡單的方法是將許多全連接層堆疊在一起,每一層都輸出到上面的層,直到生成最後的輸出。我們可以把前 L−1 層看作表示,把最後一層看作線性預測器。
這種架構通常稱為 多層感知機(multilayer perceptron)即MLP
由於仿射函數的複合還是仿射函數(明顯),所以簡單堆疊更多線性層而不做其他變換 對於非線性的學習 是毫無意義的,反而徒增參數量(雖然說並非完全無意義 hh)。
MLP 的優勢在於在仿射變換之後對每個隱藏單元應用非線性的 激活函數 activation function σ。激活函數的輸出被稱為 活性值 activations。有了激活函數,一般就不可能再將我們的多層感知機退化成線性模型。
MLP 的結構#
無需多言!
HO=σ(XW(1)+b(1)),=HW(2)+b(2).
對每個隱藏層都做一次過一次非線性的激活函數後,隱藏層堆起來就有其意義了(學習更複雜的非線性關係,從而具有更強大的表達能力)。
H(1)H(2)=σ1(XW(1)+b(1))=σ2(H(1)W(2)+b(2))⋯
隱藏層可以加廣 / 變深,但得有個取捨 (略)
激活函數們#
第一個登場的是大名鼎鼎的 ReLU 函數,雖然它看起來非常簡單,但確實是最廣泛使用的激活函數之一。
非常地簡單粗暴啊,遇到負值直接變 0,遇到正值就照抄。
ReLU(x)=max(x,0).
函數圖像略
但有一個問題,它在 x=0 的時候的導數值有一個突變(這就非常煩人了,事實上一切邊界條件都很煩人),於是我們預設 0 處的導數值為 0 hh,直接採取無所謂的態度。
有點像電路裡的整流二極管(信號要麼通過,要麼阻斷)。更重要的是它解決了神經網路的梯度消失問題()。
“那麼可不可以網開一面,保留一小部分信號通過呢?”
於是有了它的改進版 pReLU:
pReLU(x)=max(0,x)+αmin(0,x).
第二個登場的是 sigmoid 函數,sigmoid:R→(0,1)
sigmoid(x)=1+exp(−x)1.

然而,sigmoid 在隱藏層中已經較少使用, 它在大部分時候被更簡單、更容易訓練的 ReLU 所取代。 循環神經網路中利用 sigmoid 單元來控制時序信息流的架構。當輸入接近 0 時,sigmoid 函數接近線性變換。
dxdsigmoid(x)=(1+exp(−x))2exp(−x)=sigmoid(x)(1−sigmoid(x)).
(這倒是一個不錯的性質)
最後一個介紹的是 tanh 函數
tanh(x)=1+exp(−2x)1−exp(−2x).
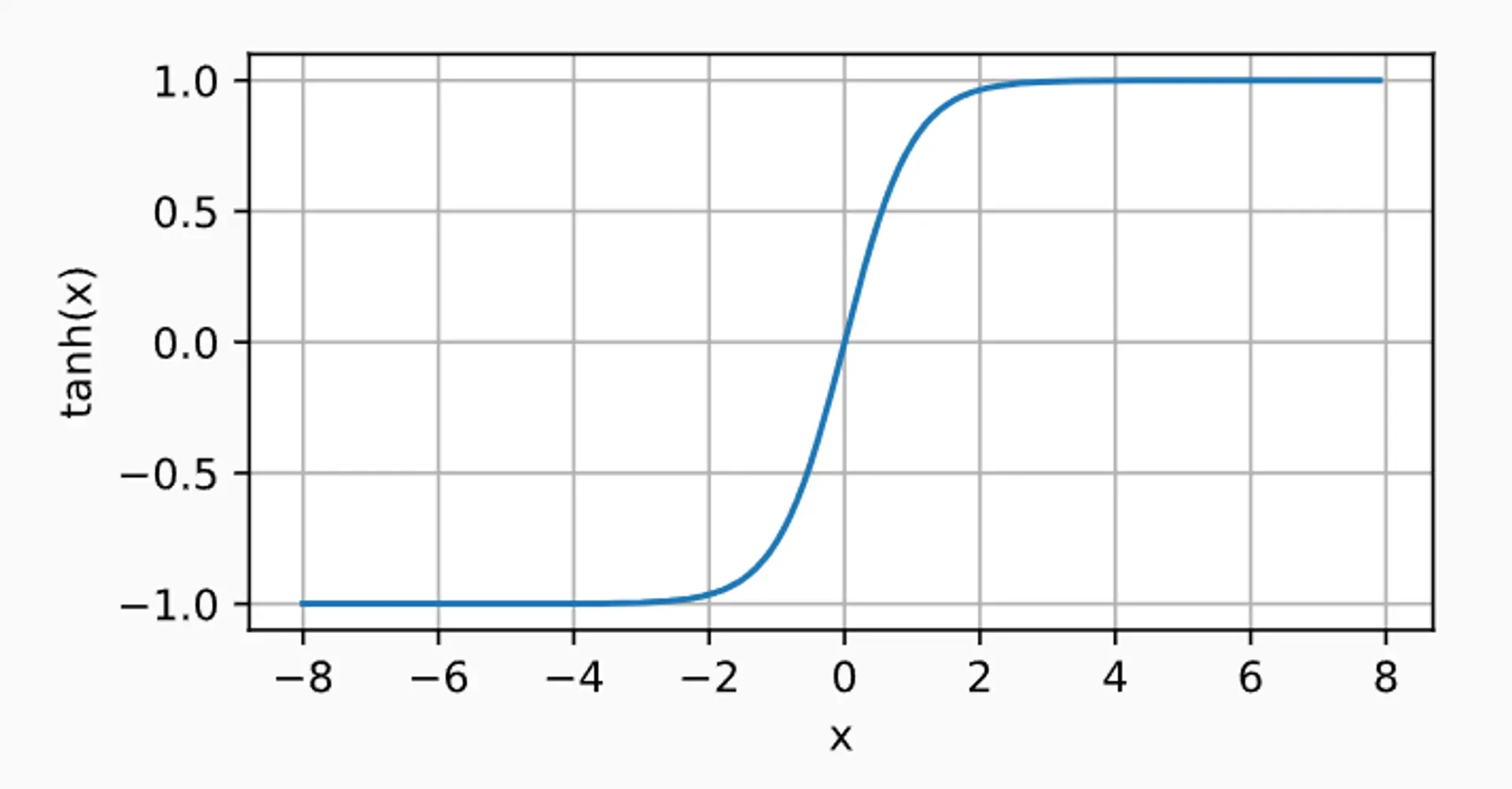
dxdtanh(x)=1−tanh2(x).
(這也是一個不錯的性質)
(虛假的)結束語#
當然會再回頭補充,但就先寫到這裡,代碼部分想另外開一個欄))
Bye~